Elementary Statistics (STAT 201)

Probability

Randomness -- flip a coin

  • A phenomenon is a random phenomenon if all possible outcomes of the phe- nomenon are known, but which one occurs is uncertain. We use probability to quantify the uncer- tainty in random phenomena.

  • A random trial or random experiment is any observable action in which the occurrence of the outcomes is random.

Random Noise

Which one is more "random" ?

  • Suppose you flipped a coin many times, H means you observed a head, T means tail.
  • Two records:
    • HTTHTTTHTTTHHTTTTHTHTTHHHTHTHTTHHHHTHHHHTTHHHHHHHHHTH THTHTHTTHTHTHHHTHHTHTTHHTTHHTHTHHTHHTHTTTTHTTHH
    • HTTHTHTHTTHTHHTHTTHTHTTHTTTHTTHTTTHTTHTHTTHTHTTHTTTHT HTHTHTTHTHTHHTHTHTHTHTHTHTHTHTTHTHTHTTTHTTHTTHT

Probability

  • The probability of an event A is the proportion of times that the event occur in a long run of observations. We often denote the probability of an event A by $P(A)$.

  • Remark. The above definition is usually referred to as the law of large numbers (LLN), which states that the sample proportion of an event A gradually approaches P(A) as the sample size n increases to infinity.

LAW of Large Numbers

In [21]:
from IPython.display import IFrame
IFrame("http://47.254.76.4:3838/sample-apps/LLN/", width=1000, height=500)
Out[21]:

Sample space and Events

  • The sample space of a random trial, denoted by S, is the collection of all possible outcomes of the trial.
  • An event is a sub-collection of some outcomes within the sample space.

Calculating the probability

  • In case the number of outcomes in S is finite, if the outcomes are all equally likely to occur, then the probability of an event A is given by
$$ P(A) =\frac{\operatorname{Number of outcomes in} A}{\operatorname{Number of outcomes in} S} = \frac{N(A)}{N(S)} $$

Basic properties

  • $P(S) = 1$

  • For any event $A$, $0 ≤ P(A) ≤ 1$

    • If $P(A) = 1$, we call the event $A$ a sure event.
    • If $P(A) = 0$, we call the event $A$ an impossible event.

  • The probabilities of all outcomes should sum to 1.

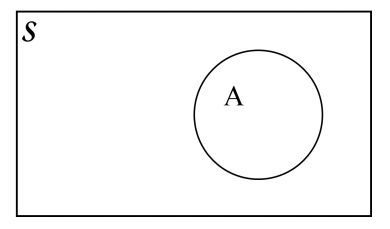
Venn diagram

  • A Venn diagram, displays the relationship between a sample space and possible events, in which
    • the rectangle represents the sample space S;
    • the circle represents a specific event A.

Basic probability rules

  • Complement $A^c$: all outcomes in the sample space $S$ that do not belong to the event $A$.
$$ P(A^c) = 1 − P(A) $$
  • Disjoint events: two events, $A$ and $B$, are disjoint if they do not share any common outcomes. If events $A$ and $B$ are disjoint,

Basic probability rules

  • Intersection $A$ and $B$: all outcomes in the sample space S that belong to both $A$ and $B$.
$$ P(A \operatorname{and} B) = \frac{N(A \operatorname{and} B)}{N(S)} = \frac{\operatorname{Number of outcomes in} A \operatorname{and} B}{\operatorname{Number of outcomes in} S} $$
  • Union $A$ or $B$: all outcomes in the sample space S that belong to both $A$ or $B$.
$$ P(A \operatorname{or} B) = P(A) + P(B) − P(A \operatorname{and} B) $$

Basic probability rules

  • If events A and B are disjoint, then we have

    • $$ P(A \operatorname{and} B) = 0 $$

    • $$ P(A \operatorname{or} B) = P(A) + P(B) $$

Basic probability rules - explained by Venn diagram

  • Intersection

Basic probability rules - explained by Venn diagram

  • Union

Exercise time!

Conditional probability

  • For events $A$ and $B$, the conditional probability of event $A$ given that event $B$ has occurred is

    $$ P(A | B) = \frac{P(A \operatorname{and} B)}{P(B)} = \frac{\operatorname{Number of outcomes in} A \operatorname{and} B}{\operatorname{Number of outcomes in} B} $$

  • $P (A|B)$ is read as “the probability of event A given event B”. The pipe “|” represents the word “given”.

  • The formula above can alos be written as : $$ P(A \operatorname{and} B) = P (A|B) · P(B) = P (B|A) · P(A) $$

Independence

  • Two events A and B are statistically independent if the occurrence of one event is not affected by whether the other event has already occurred.

  • $A$ and $B$ are statistically independent if one of the following is satisfied:

    • $$ P(A | B) = P(A) $$
    • $$ P(B | A) = P(B) $$
    • $$ P(A \operatorname{and} B) = P(A) · P(B) $$

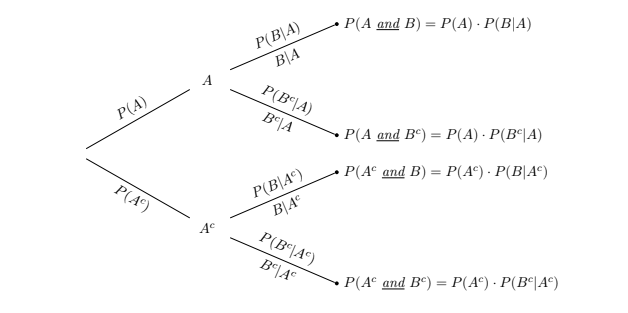
Tree diagram

  • We can summarize the probabilities of two events A and B into a tree diagram. The process of creating a tree diagram is as the following:

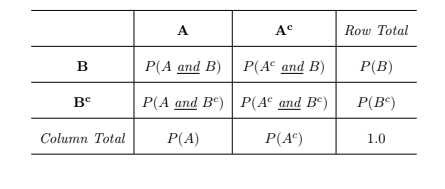
2 - by - 2 contigency table

  • Further, we can arrange the intersection probabilities into the 2 × 2 contingency table below.

Clinical example

  • In clinical studies, an individual has a true identity of whether or not s/he has a certain disease. At the same time, a medical test on the blood sample (or any other sample) taken from the individual can be positive or negative. Let events

    • $D$ = the individual has the disease

    • $D^c$ = the individual does not have the disease

    • $+$ = the test result is positive

    • $-$ = the test result is negative

Clinical example

  • Then we have the following terminologies:

    • The prevalence of a disease, $P(D)$, is the probability of the disease, or how popular the disease is among a group of people.

    • The sensitivity of a medical test, $P(+|D)$, is the probability of a positive test result given the individual actually has the disease.

    • The specificity of a medical test, $P(−|D^c)$, is the probability of a negative test result given the individual actually does not have the disease.

Some other terminologies:

Events $D$ $D^c$
$+$ True Positives False Positives
$-$ False Negatives True Negatives

END